Algoritmos Numéricos
La eliminacion de Gauss-Jordan es un algoritmo numérico usado para una gran cantidad de casos específicos, aunque posterioremente se han desarrollado algoritmos alternativos mucho más eficientes. La mayoría de estos algoritmos mejorados tienen una complejidad computacional de O(n²) (donde n es el número de ecuaciones del sistema). Algunos de los métodos más usados son:
·Para los problemas de la forma Ax = b, donde A es una matriz de Toeplitz simétrica, se puede utilizar la recursion de Levinson o alguno de los métodos derivados de este. Un método derivado de la recursión de Levinson es la recursión de Schur, que es ampliamente usado en el campo del procesamiento digital de señales.
·Para los problemas de la forma Ax = b, donde A es una matriz singular o casi singular, la matriz A se descompone en el producto de tres matrices en un proceso llamado descomposicion en valores singulares.
Cuando consideramos ecuaciones lineales cuyas soluciones son números racionales, reales o complejos o más generalmente un cuerpo 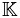 , la solución puede encontrarse mediante regla de Cramer. Para sistemas de muchas ecuaciones la regla de Cramer puede ser computacionalmente más costosa y suelen usarse otros métodos más "económicos" en número de operaciones como la eliminacion de Gauss-Jordan y la descomposicion de Cholesky. Existen también métodos indirectos (basados en iteraciones) como el metodo de Gauss-Seidel
, la solución puede encontrarse mediante regla de Cramer. Para sistemas de muchas ecuaciones la regla de Cramer puede ser computacionalmente más costosa y suelen usarse otros métodos más "económicos" en número de operaciones como la eliminacion de Gauss-Jordan y la descomposicion de Cholesky. Existen también métodos indirectos (basados en iteraciones) como el metodo de Gauss-Seidel
Si el cuerpo es infinito (como es el caso de los números reales o complejos), entonces solo puede darse una de las tres siguientes situaciones:
·el sistema no tiene solución (en dicho caso decimos que el sistema está sobredeterminado o que es incompatible)
·el sistema tiene una única solución (el sistema es compatible determinado)
·el sistema tiene un número infinito de soluciones (el sistema es compatible indeterminado).
